Proporsi
Proporsi mengatakan bahwa dua rasio (atau pecahan) adalah sama.
Contoh:
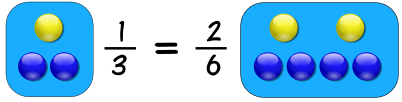
Jadi 1-dari-3 sama dengan 2-dari-6
Rasionya sama, jadi proporsional.
Contoh: Tali
Panjang dan berat tali proporsional.
Jika tali 20m beratnya 1kg , maka:
- Tali 40m itu beratnya 2kg
- 200m tali itu beratnya 10kg
- dll.
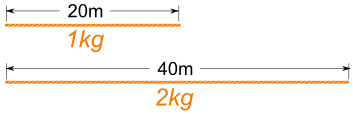
Begitu:
201 = 402
Ukuran
Saat bentuk "proporsional", ukuran relatifnya sama.
Di sini kita melihat bahwa rasio panjang kepala dan panjang badan sama pada kedua gambar. Jadi proporsional . Membuat kepala terlalu panjang atau pendek akan terlihat buruk! | 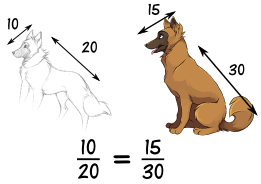 |
Contoh: Ukuran kertas internasional (seperti A3, A4, A5, dll) semuanya memiliki proporsi yang sama:

Jadi setiap karya seni atau dokumen dapat diubah ukurannya agar sesuai dengan lembar apa pun. Sangat rapi.
Bekerja Dengan Proporsi
SEKARANG, bagaimana kita menggunakan ini?
Contoh: Anda ingin menggambar kepala anjing ... berapa panjangnya?
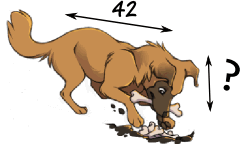
Mari kita tulis proporsinya dengan bantuan rasio 10/20 dari atas:
?42 = 1020
Sekarang kami menyelesaikannya menggunakan metode khusus:

Kalikan di sudut-sudut yang diketahui,
lalu bagi dengan angka ketiga
Dan kami mendapatkan ini:
? = (42 × 10) / 20
= 420/20
= 21
Jadi, Anda harus menggambar panjang kepala 21 .
Menggunakan Proporsi untuk Memecahkan Persen
Persen sebenarnya adalah rasio! Mengatakan "25%" sebenarnya mengatakan "25 per 100":
25% = 25100
Kita dapat menggunakan proporsi untuk menyelesaikan pertanyaan yang melibatkan persen.
Triknya adalah memasukkan apa yang kita ketahui ke dalam formulir ini:
BagianSeluruh = Persen100
Contoh: Berapa 25% dari 160?
Persennya 25, keseluruhan 160, dan kami ingin mencari "bagian":
Bagian160 = 25100
Kalikan di sudut-sudut yang diketahui, lalu bagi dengan angka ketiga:

Bagian = (160 × 25) / 100
= 4000/100
= 40
Jawaban: 25% dari 160 adalah 40.
Catatan: kita juga bisa menyelesaikan ini dengan melakukan pembagian terlebih dahulu, seperti ini:
Bagian = 160 × (25/100)
= 160 × 0.25
= 40
Metode mana pun berfungsi dengan baik.
Kami juga dapat menemukan Persen:
Contoh: berapa $ 12 sebagai persen dari $ 80?
Isi apa yang kami ketahui:
$ 12$ 80 = Persen100
Kalikan di sudut-sudut yang diketahui, lalu bagi dengan angka ketiga. Kali ini sudut yang diketahui adalah kiri atas dan kanan bawah:

Persen = ($ 12 × 100) / $ 80
= 1.200 / 80
= 15%
Jawaban: $ 12 adalah 15% dari $ 80
Atau temukan Seluruhnya:
Contoh: Harga jual ponsel adalah $ 150, yang mana hanya 80% dari harga normal. Berapa harga normalnya?
Isi apa yang kami ketahui:
$ 150Seluruh = 80100
Kalikan di sudut-sudut yang diketahui, lalu bagi dengan angka ketiga:

Keseluruhan = ($ 150 × 100)
/ 80
= 15000/80 = 187,50
Jawaban: harga normal telepon adalah $ 187,50
Menggunakan Proporsi untuk Memecahkan Segitiga
Kita dapat menggunakan proporsi untuk menyelesaikan segitiga serupa.
Contoh: Berapa tinggi Pohon itu?
Sam mencoba menggunakan tangga, pita pengukur, tali, dan berbagai benda lainnya, tetapi tetap tidak bisa menentukan tinggi pohon itu.
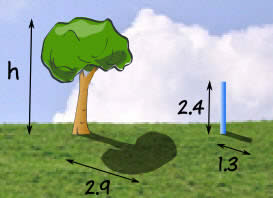
Tapi kemudian Sam punya ide cerdas ... segitiga serupa!
Sam mengukur tongkat dan bayangannya (dalam meter), dan juga bayangan pohon, dan inilah yang didapatnya:
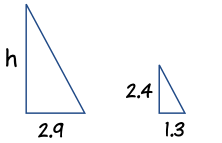
Sekarang Sam membuat sketsa segitiga, dan menuliskan rasio "Tinggi terhadap Panjang" untuk kedua segitiga:
Tinggi:Panjang Bayangan: h2,9 m = 2,4 m1,3 m
Kalikan di sudut-sudut yang diketahui, lalu bagi dengan angka ketiga:
h = (2,9 × 2,4) / 1,3
= 6,96 / 1,3
= 5,4 m (ke terdekat 0,1)
Jawaban: tinggi pohon 5,4 m.
Dan dia bahkan tidak membutuhkan tangga!
"Ketinggian" bisa saja di bagian bawah, selama berada di bagian bawah untuk KEDUA rasio, seperti ini:

Mari kita coba rasio "Panjang Bayangan ke Tinggi":
Panjang Bayangan:Tinggi: 2,9 mh = 1,3 m2,4 m
Kalikan di sudut-sudut yang diketahui, lalu bagi dengan angka ketiga:
h = (2,9 × 2,4) / 1,3
= 6,96 / 1,3
= 5,4 m (ke terdekat 0,1)
Perhitungannya sama seperti sebelumnya.
Contoh "Beton"
Rasio bisa memiliki lebih dari dua angka !
Misalnya beton dibuat dengan mencampurkan semen, pasir, batu dan air.

Campuran khas semen, pasir dan batu dituliskan sebagai perbandingan, misalnya 1: 2: 6 .
Kita bisa mengalikan semua nilai dengan jumlah yang sama dan tetap memiliki rasio yang sama.
10:20:60 sama dengan 1: 2: 6
Jadi bila kita menggunakan 10 ember semen, sebaiknya menggunakan 20 pasir dan 60 batu.
Contoh: Anda baru saja memasukkan 12 ember batu ke dalam mixer, berapa banyak semen dan berapa banyak pasir yang harus Anda tambahkan untuk membuat campuran 1: 2: 6 ?
Mari kita letakkan di tabel agar lebih jelas:
| | Semen | Pasir | Batu |
|---|
| Rasio yang Dibutuhkan: | 1 | 2 | 6 |
|---|
| Kamu punya: | | | 12 |
|---|
Anda memiliki 12 ember batu tetapi rasionya menunjukkan 6.
Tidak apa-apa, Anda hanya memiliki dua kali lebih banyak batu daripada angka dalam rasio ... jadi Anda perlu dua kali lebih banyak dari semuanya untuk menjaga rasio.
Inilah solusinya:
| | Semen | Pasir | Batu |
|---|
| Rasio yang Dibutuhkan: | 1 | 2 | 6 |
|---|
| Kamu punya: | 2 | 4 | 12 |
|---|
Dan rasio 2: 4: 12 sama dengan 1: 2: 6 (karena mereka menunjukkan ukuran relatif yang sama )
Jadi jawabannya adalah: tambahkan 2 ember Semen dan 4 ember Pasir. (Anda juga membutuhkan air dan banyak pengadukan ....)
Mengapa rasio mereka sama? Nah, rasio 1: 2: 6 mengatakan memiliki :
- Pasir dua kali lebih banyak dari Semen ( 1 : 2 : 6)
- 6 kali lebih banyak Batu dari Semen ( 1 : 2: 6 )
Dalam campuran kami, kami memiliki:
- Pasir dua kali lebih banyak dari Semen ( 2 : 4 : 12)
- 6 kali lebih banyak Batu dari Semen ( 2 : 4: 12 )
Jadi itu harus benar!
Itu adalah hal yang baik tentang rasio. Anda bisa membuat jumlahnya lebih besar atau lebih kecil dan selama ukurannya relatif sama maka rasionya sama.
Sumber : https://www.mathsisfun.com/








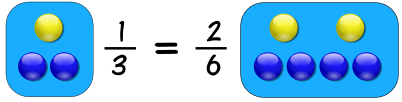












0 comments:
Post a Comment