Teorema Pythagoras Belajar Mudah dan Praktis (Kelas 8 SMP)

 Lebih dari 2000 tahun yang lalu, ada penemuan menakjubkan tentang segitiga:

Jika segitiga memiliki sudut siku-siku (90 °) ...

... dan persegi dibuat di masing-masing dari tiga sisi, ...

... maka persegi terbesar memiliki luas yang sama persis dengan gabungan dua kotak lainnya!

Ini disebut "Teorema Pythagoras" dan dapat ditulis dalam satu persamaan singkat:

a ² + b ² = c ²

catatan:

• c adalah sisi segitiga terpanjang
• a dan b adalah dua sisi lainnya

Definisi

Sisi terpanjang segitiga disebut "hipotenusa", jadi definisi formalnya adalah:

Dalam segitiga siku-siku:
kuadrat hipotenusa sama dengan
jumlah kuadrat dari dua sisi lainnya.

Tentu ... ?

Mari kita lihat apakah itu benar-benar berfungsi dengan menggunakan contoh.

Contoh: Segitiga "3,4,5" memiliki sudut siku-siku di dalamnya.

Mari kita cek jika daerah yang sama: 3 2 + 4 2 = 5 2 Menghitung ini menjadi: 9 + 16 = 25 Ia bekerja ... seperti Sihir!

Mengapa Ini Berguna?

Jika kita mengetahui panjang dua sisi segitiga siku-siku, kita bisa mencari panjang sisi ketiganya . (Tapi ingat, ini hanya berfungsi pada segitiga siku-siku!)

Bagaimana Saya Menggunakannya?

Tuliskan sebagai persamaan:

a 2 + b 2 = c 2

Kemudian kami menggunakan aljabar untuk menemukan nilai yang hilang, seperti dalam contoh berikut:

Contoh: Pecahkan segitiga ini

Dimulai dari:a ² + b ² = c ²

Masukkan apa yang kami ketahui:5 ² + 12 ² = c ²

Hitung kotak:25 + 144 = c ²

25 + 144 = 169:169 = c ²

Tukar sisi:c ² = 169

Akar kuadrat dari kedua sisi:c = √169

Menghitung:c = 13

Contoh: Pecahkan segitiga ini.

Dimulai dari:a ² + b ² = c ²

Masukkan apa yang kami ketahui:9 ² + b ² = 15 ²

Hitung kotak:81 + b ² = 225

Ambil 81 dari kedua sisi:81 - 81 + b ² = 225 - 81

Menghitung:b ² = 144

Akar kuadrat dari kedua sisi:b = √144

Menghitung:b = 12

Contoh: Berapa jarak diagonal pada persegi berukuran 1?

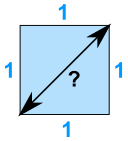
Dimulai dari:a ² + b ² = c ²

Masukkan apa yang kami ketahui:1 ² + 1 ² = c ²

Hitung kotak:1 + 1 = c ²

1 + 1 = 2:2 = c ²

Tukar sisi:c ² = 2

Akar kuadrat dari kedua sisi:c = √2

Yaitu tentang:c = 1,4142 ...

Ini juga berlaku sebaliknya: ketika tiga sisi segitiga membentuk a ² + b ² = c ² , maka segitiga itu bersudut siku-siku.

Contoh: Apakah segitiga ini memiliki Sudut Siku?

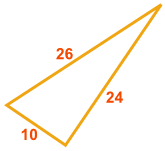
Apakah a ² + b ² = c ² ?

• a ² + b ² = 10 ² + 24 ² = 100 + 576 = 676
• c ² = 26 ² = 676

Mereka setara, jadi ...

Ya, itu memang memiliki Sudut siku - siku!

Contoh: Apakah segitiga 8, 15, 16 memiliki Sudut Siku-siku?

Apakah 8 ² + 15 ² = 16 ² ?

• 8 ² + 15 ² = 64 + 225 = 289 ,
• tetapi 16 ² = 256

Jadi, TIDAK, itu tidak memiliki sudut siku - siku

Contoh: Apakah segitiga ini memiliki Sudut siku - siku?

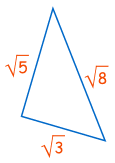
Apakah a ² + b ² = c ² ?

Apakah ( √ 3) ² + ( √ 5) ² = ( √ 8) ² ?

Apakah 3 + 5 = 8?

Ya, benar!

Jadi ini adalah sebuah segitiga siku-siku

Sumber : https://www.mathsisfun.com/pythagoras.html