Bagaimana Cara Menentukan Bilangan Prima dengan Metode Saringan Eratosthenes

Dalam postingan hari ini, kita akan mempelajari cara menemukan bilangan prima menggunakan Saringan Eratosthenes.

Bilangan prima adalah bilangan yang hanya habis dibagi 1 dan bilangan itu sendiri. Semudah itu; sisi negatifnya adalah tidak ada rumus matematika untuk memastikan apakah suatu bilangan prima atau bukan.

Pikirkan bilangan yang besar seperti 191.587. Kita tidak memiliki rumus untuk menentukan apakah itu bilangan prima atau tidak!

Kita harus mencari tahu apakah ia memiliki pembagi, dan oleh karena disebut dengan komposit. Dalam kasus ini, kita akan membuangnya dari bilangan prima.

Sangat mudah untuk memeriksa apakah beberapa bilangan prima pertama (2, 3, 5, 7, 11) memiliki pembagi menggunakan bantuan kriteria pembagian. Tetapi tidak mudah untuk jumlah yang lebih besar.

Bayangkan harus memeriksa semua pembagi dari angka yang begitu besar! Ini akan gila!

Saringan Eratosthenes

Ahli matematika Yunani Eratosthenes (abad ke-3 SM) merancang cara cepat untuk mencari semua bilangan prima. Ini adalah proses yang disebut Saringan Eratosthenes. 

Kita akan melihat cara kerjanya dengan mencari semua bilangan prima antara 1 dan 100.

Idenya adalah untuk menemukan bilangan dalam tabel yang merupakan kelipatan dari suatu bilangan dan karenanya disebut komposit, lalu dibuang dari bilangan prima. 

Bilangan yang tersisa akan menjadi bilangan prima.

Saringan Eratosthenes berhenti ketika kuadrat dari angka yang kita uji lebih besar dari angka terakhir pada grid (dalam kasus ini kita ambil 100).

Karena 112 = 121 dan 121> 100, saat kita sampai ke angka 11, kita bisa berhenti mencari.

Bilangan prima antara 1 dan 100 dengan Saringan Eratosthenes

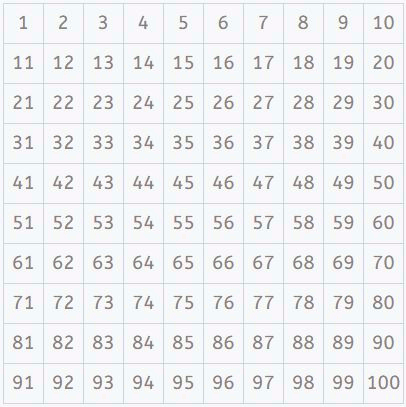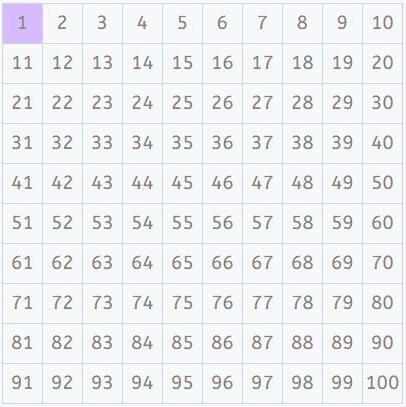
Kita mulai dengan menempatkan angka dari 1 hingga 100 dalam tabel seperti ini. Dengan cara ini, sangat mudah untuk melihat pola yang dibuat oleh kelipatan setiap angka. Kita menyoroti 1, yang bukan bilangan prima.

Pertama, kita mencari kelipatan 2 dan menyorotnya (menyisakan 2, karena kita tahu bahwa ia hanya memiliki pembagi 1 dan 2 dan oleh karena itu bilangan prima). Semua nomor yang disorot akan menjadi gabungan. Pernahkah Anda melihat pola indah yang dibuat oleh bilangan genap?

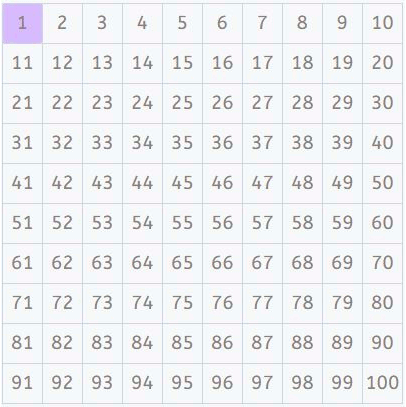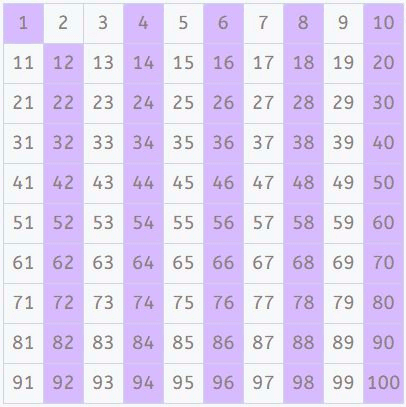
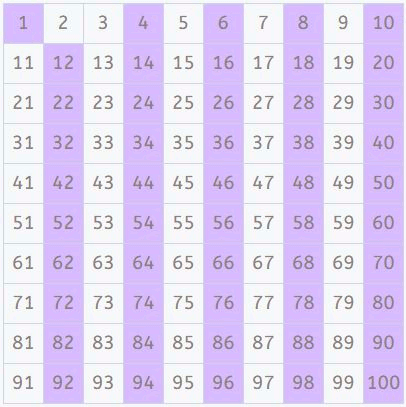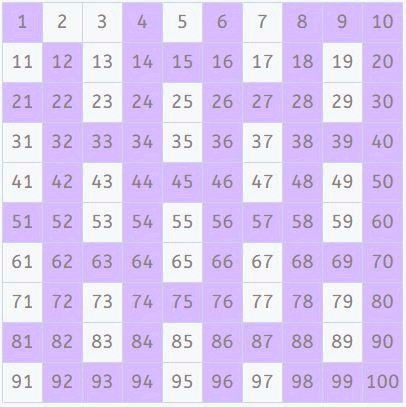
Sekarang, dari bilangan yang tersisa, kita mencari kelipatan 3 dan menyorotnya (kecuali 3, karena bilangan prima). Cara yang mudah untuk melakukannya adalah dengan menghitung bertiga. Kita mendapatkan pola menarik lainnya setelah selesai.

Sekarang waktunya mencari kelipatan 5. Kita tidak perlu mencari kelipatan 4, karena semua perkalian 4 juga merupakan kelipatan 2, jadi kita sudah menyorotnya. Mudah untuk menemukan kelipatan 5, semuanya diakhiri dengan 0 atau 5. Kami tidak menyoroti 5, karena itu bilangan prima.

Mari beralih ke kelipatan 7 (6 = 2 x 3 dan kita sudah menemukan kelipatan 2 dan 3). Kita tidak menyoroti 7 karena itu yang prima.

Apakah kita harus mencari kelipatan 8, 9 dan 10? Karena bilangan ini adalah gabungan dan kelipatan dari bilangan yang sudah kita cari, kita bisa lanjut ke bilangan 11. Kita sudah tentukan bahwa kita berhenti di angka 11, jadi itu artinya kita sudah selesai!

Daftar bilangan prima antara 1 dan 100

Oleh karena itu, kita dapat menentukan bahwa bilangan yang belum kita soroti semuanya adalah bilangan prima. Jadi sekarang kita memiliki daftar bilangan prima antara 1 dan 100:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, dan 97 .

Lihat betapa mudahnya mencari bilangan prima dengan cara ini?

Terakhir, di sini kalian memiliki gambar termasuk semua langkah yang kita lihat dalam contoh, sehingga kalian dapat melihat semuanya bersama-sama.

Apakah kalian menikmati postingan ini? Tahukah kalian tentang Saringan Eratosthenes? Kalian dapat melakukan apa yang telah kita lakukan di postingan ini dengan mencoret bilangan yang bukan bilangan prima.

Source : https://www.smartickmethod.com